After fixing a bug in how I was implementing my prior in the unfolding process, I updated the spectra I previously unfolded and also tried unfolding some new spectra.  The uncertainty bands below contain the following:

• Default unfolding [bayesian algo., k = 4 (for R = 0.2) or 5 (for R = 0.5), embedding response, prior is taken from Pythia 6]
• Parameterization of the response [i.e. using Pythia 8 as the prior]
• +-5% on the tracking efficiency
• 2 variations of the tracking resolution
• k + 1
• Levy prior
• Power law prior, +-0.2 on the "default power" [taken from fits to Pythia 8]

And just to be clear, the algorithm for calculating the gamma-direct systematic uncertainties is as so:

1. Given a systematic variation and the default, do the gamma-rich bkgd. subtraction so that 'YdirDef = (YrichDef - B * YpiDef) / (1 - B)' and 'YdirVar = (YrichVar - B * YpiVar) / (1 - B)'.  Here 'Y' indicates the per-trigger yield for a given triggered recoil-jet spectrum, and 'B' indicates the gamma-rich background level.
2. Re-do gamma-rich subtraction for both the default and variation with 'B + deltaB' and 'B - deltaB' to obtain 3 (in total) variations of 'YdirVar' and 2 variations (besides the default) of 'YdirDef'.  Here 'deltaB' indicates the total uncertainty on 'B'.
3. Calculate the systematic uncertainty between 'YdirDef' and all 5 variations of 'YdirVar' and 'YdirDef'.
4. Repeat for all systematic varations.

The systematic uncertainty calculation is handled in the same manner as before.  Below are some examples of the systematic uncertainties on the gamma-direct trigger.

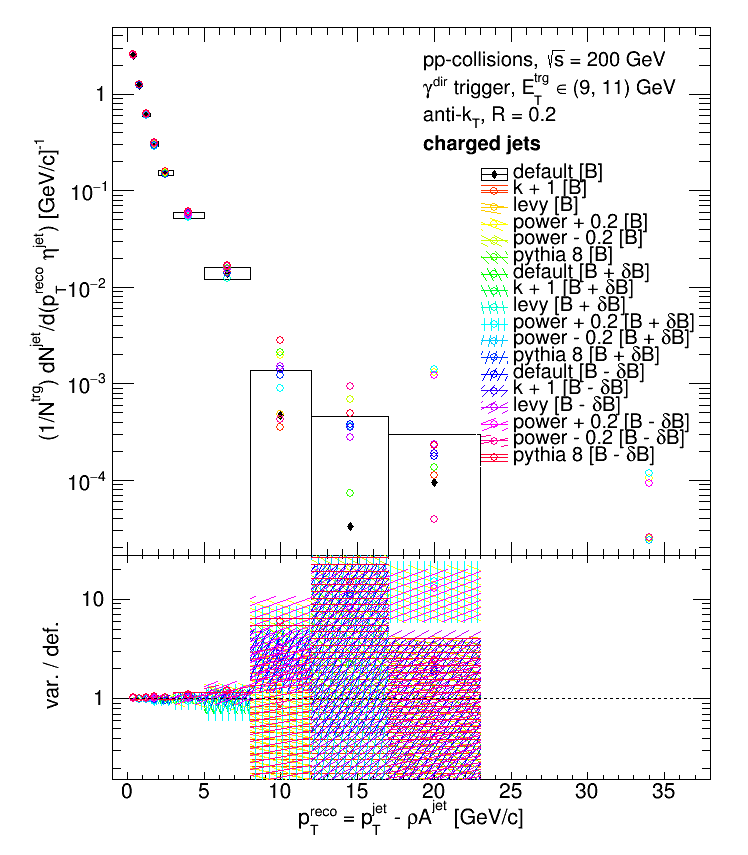
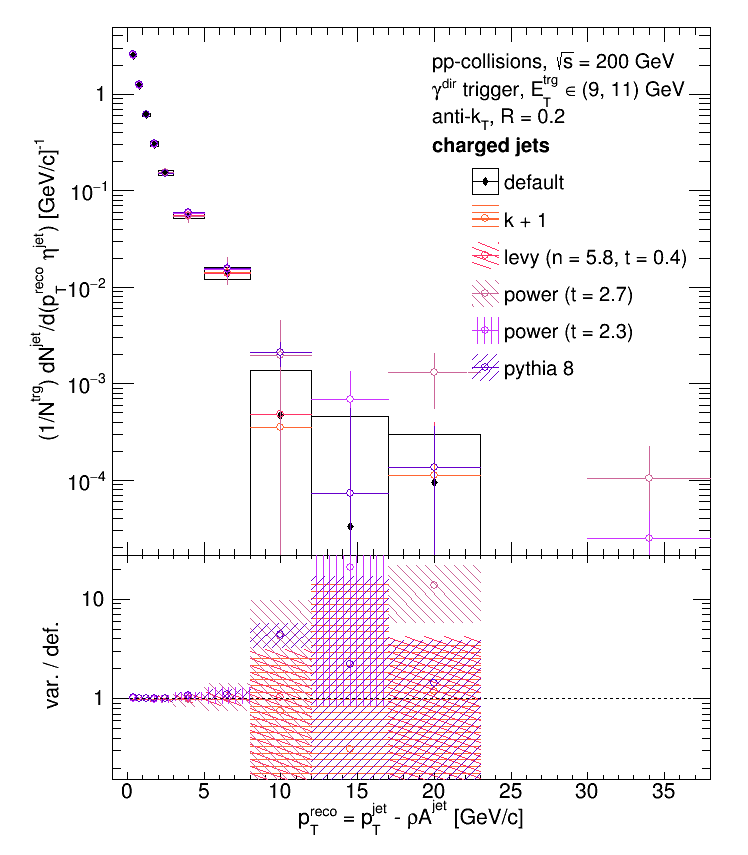
Note that the common errors have not been removed from the ratios.  And so, below are the fully corrected results.

R = 0.2, eTtrg = 9 - 11 GeV:

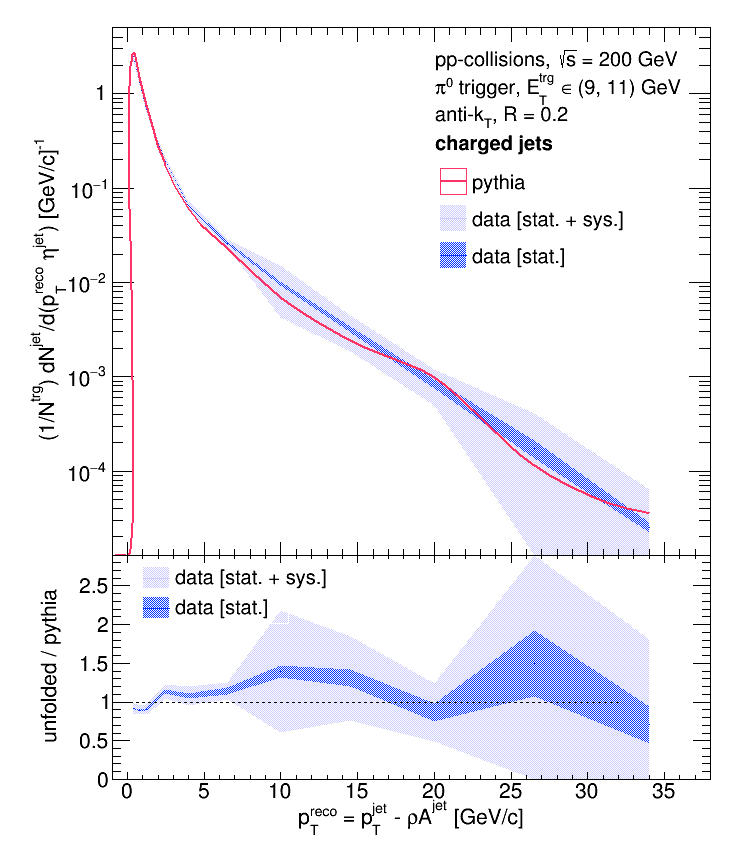
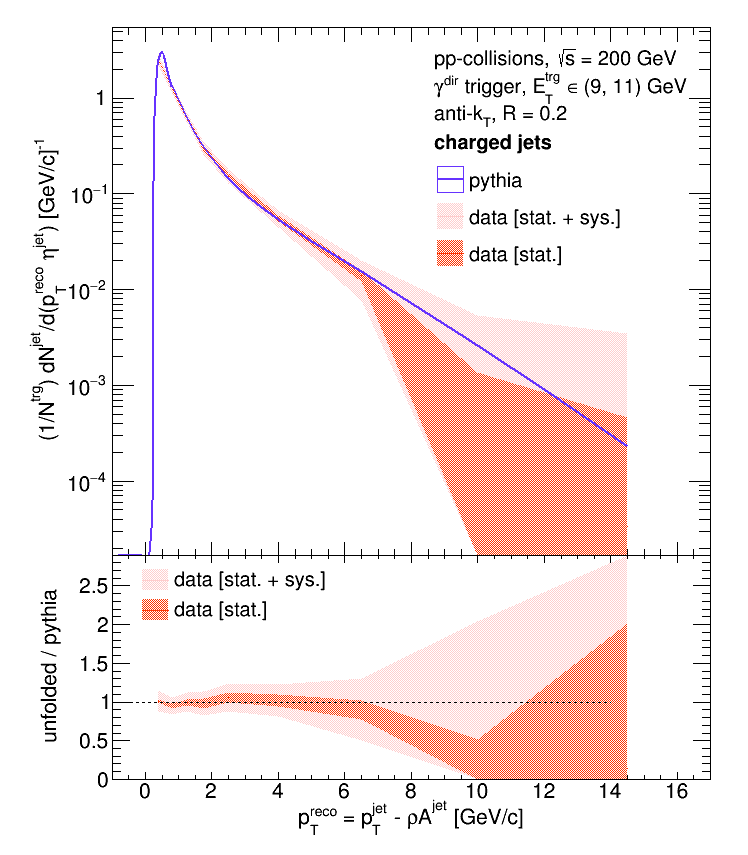
R = 0.5, eTtrg = 9 - 11 GeV:

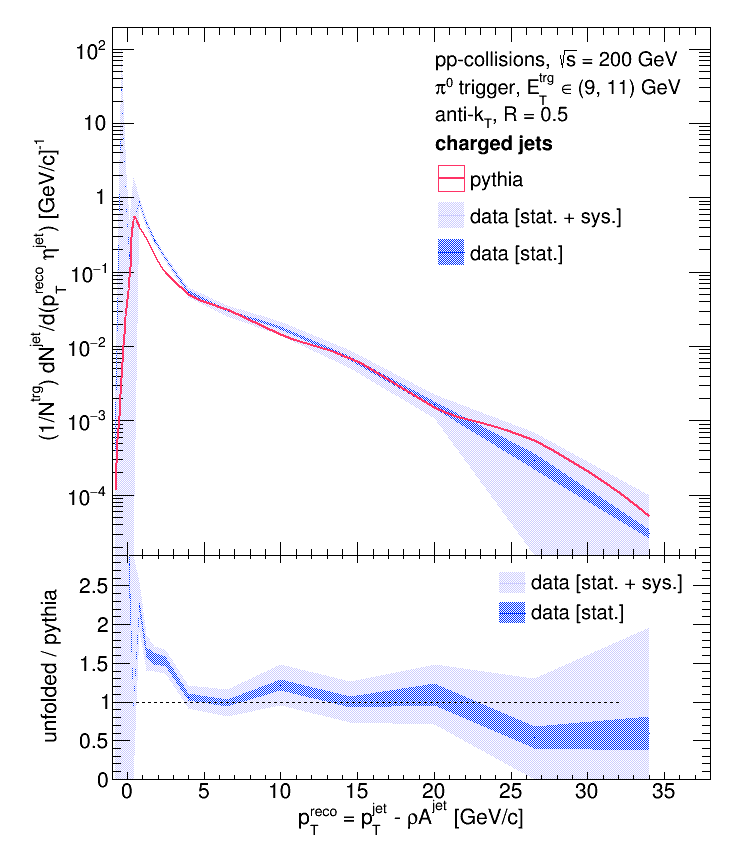
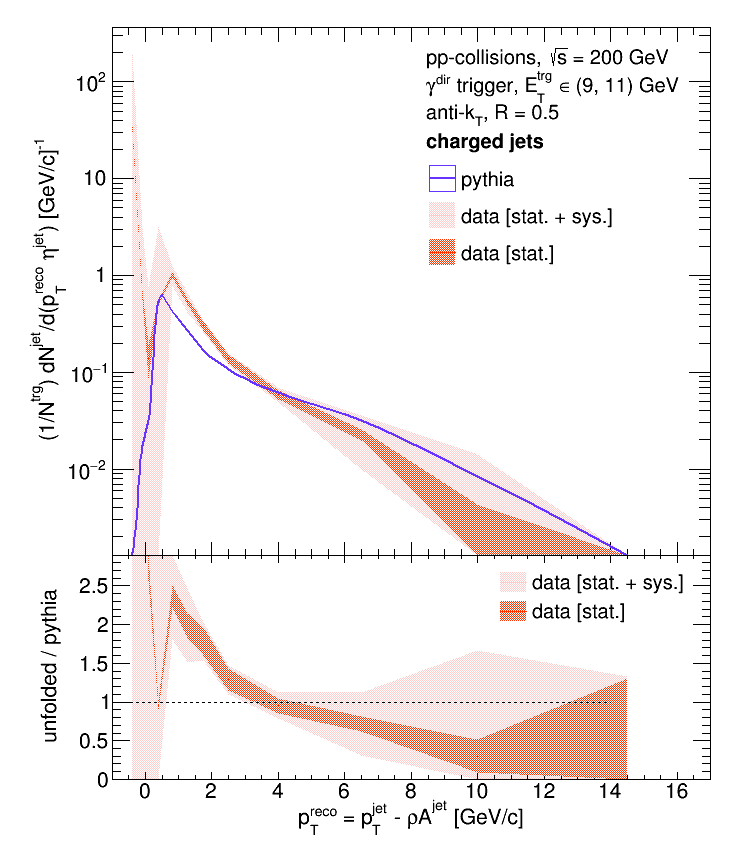
R = 0.2, eTtrg = 11 - 15 GeV:

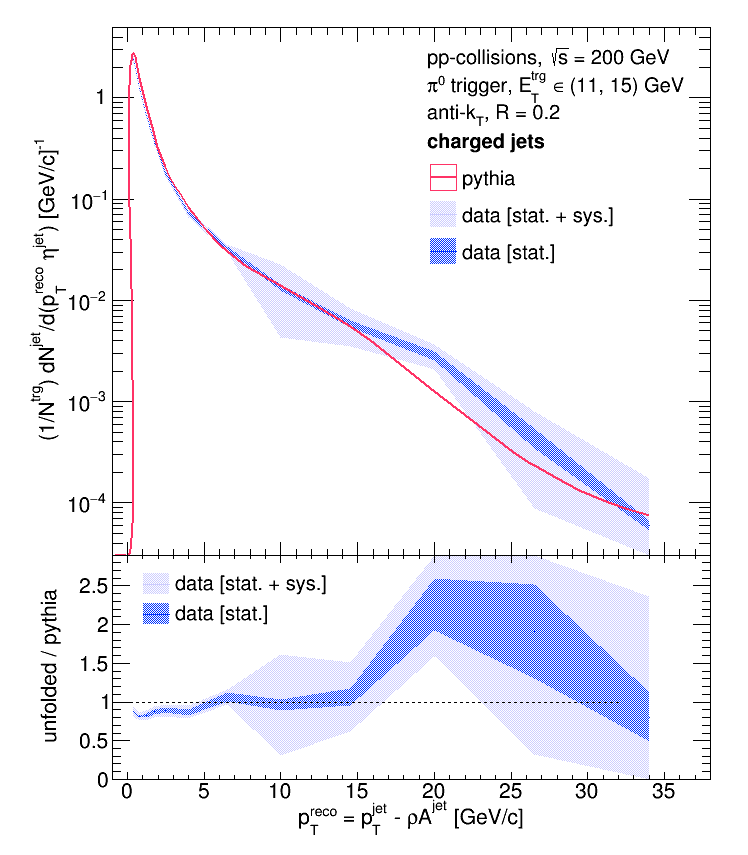
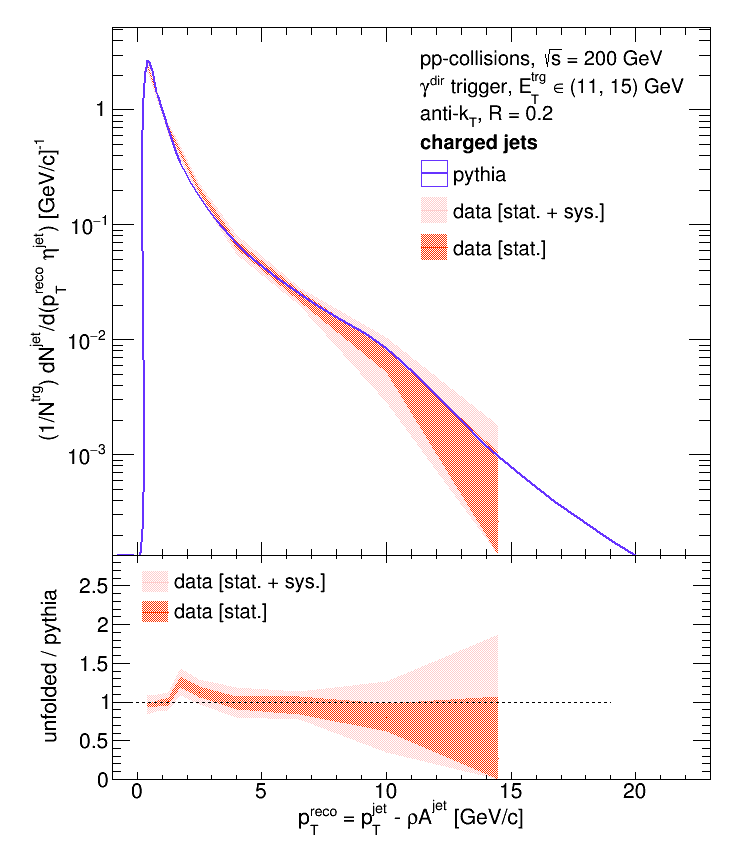
R = 0.5, eTtrg = 11 - 15 GeV:

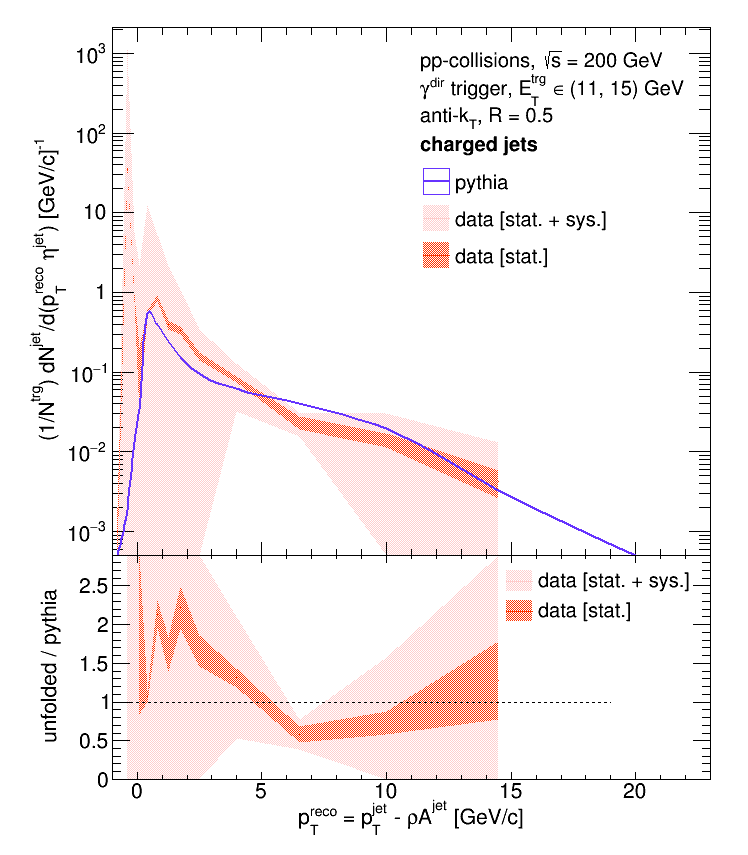
The Pythia distributions are particularly wiggly because they were made with fairly low statistics (I didn't have the relevant distributions on hand and had to churn them out quickly).