After re-establishing my binning (see the link below), I tried varying the prior used in the unfolding process to get an idea of the corresponding systematic error.

https://drupal.star.bnl.gov/STAR/blog/dmawxc/collaboration-meeting-follow-07182018-variable-binning-according-jet-energy-resolution

I used two priors: a Levy function, 'L(pT)', and an exponential, 'E(pT)'.  These are defined as so:

L(pT) = b * [(2pi * pT) / (1 + ((mT - m) / (n * t)))^n]
E(pT) = b * exp[-pT / t]

Where 'b' is an arbitrary normalization, 'mT = sqrt[pT^2 + m^2]', and 'm' is taken to be the mass of the pion (140 MeV).  For each, I then varied 'n' and 't' between these values:

n = {3.8, 4.8, 5.8, 6.8, 7.8}
t = {0.4, 1.4, 2.4, 3.4, 4.4}

The "smeared prior" was then created by convoluting each prior with our response matrix and applying our jet matching efficiency.  For each prior, I then unfolded our Run 9 pp (pi0-triggered) charged jet spectrum using the Bayesian algorithm for 'k' between 1 and 5 and selected the result with the best chi2 between the backfolded and measured distributions.  These are results:

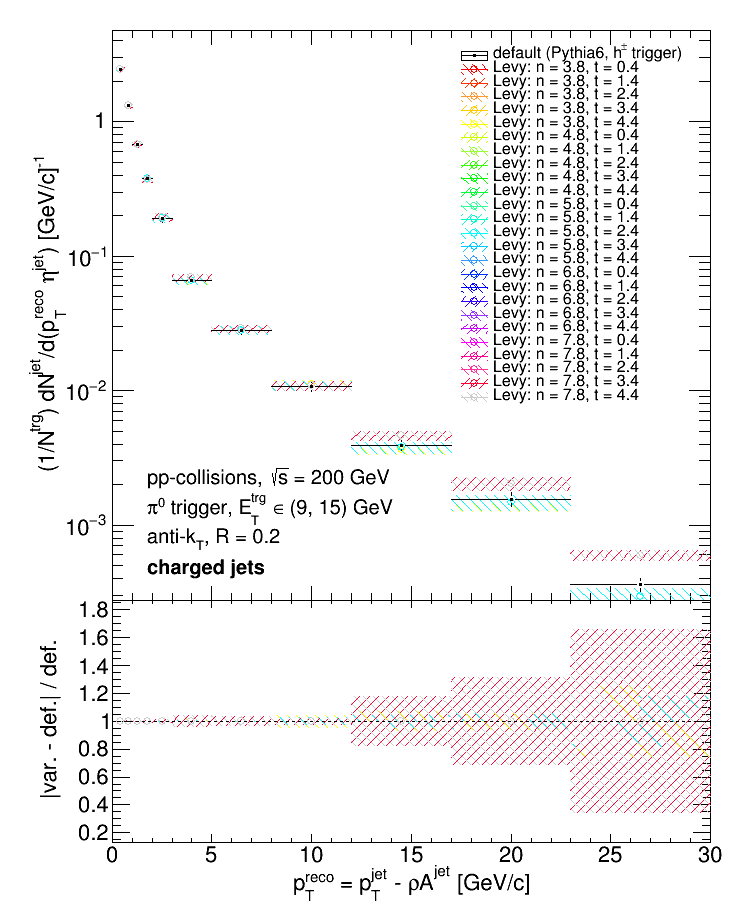
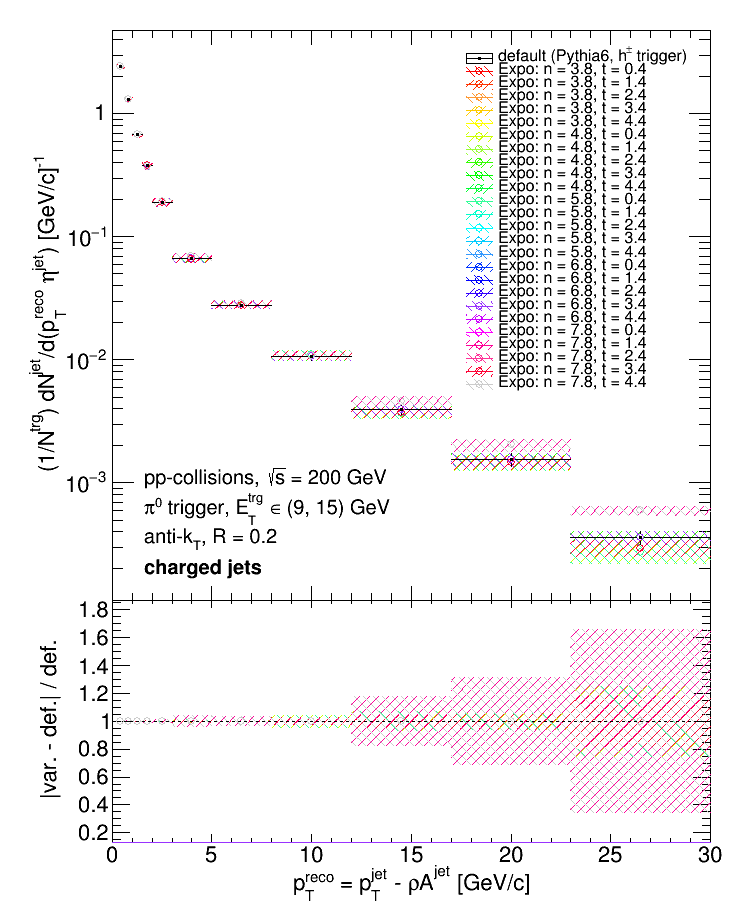
The top panels show the unfolded distributions, and the lower panel shows the %-difference between each unfolded result and the "default" result (the unfolded data using the h+- triggered Pythia6 distributions as priors, the Bayesian algorithm, and 'k = 3').  The %-difference is the difference between the central values of the unfolded distributions and the central value of the default distribution, i.e.

diff = |unfold - default| / default

and is represented as error bars about a value of 1.  Below are some examples of different priors vs. the measured, unfolded, and backfolded distributions.

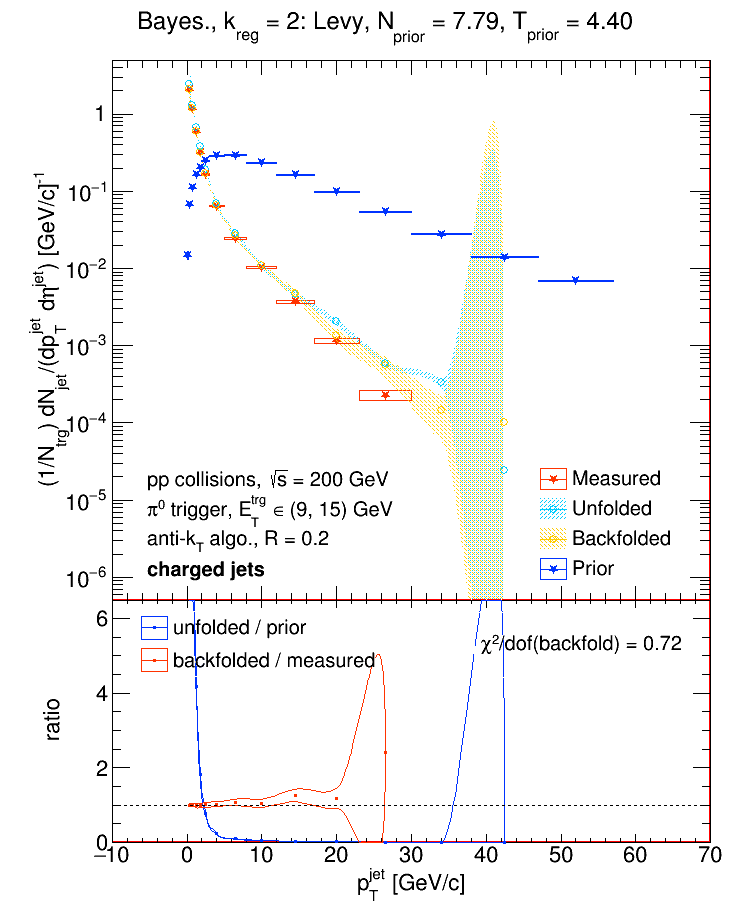
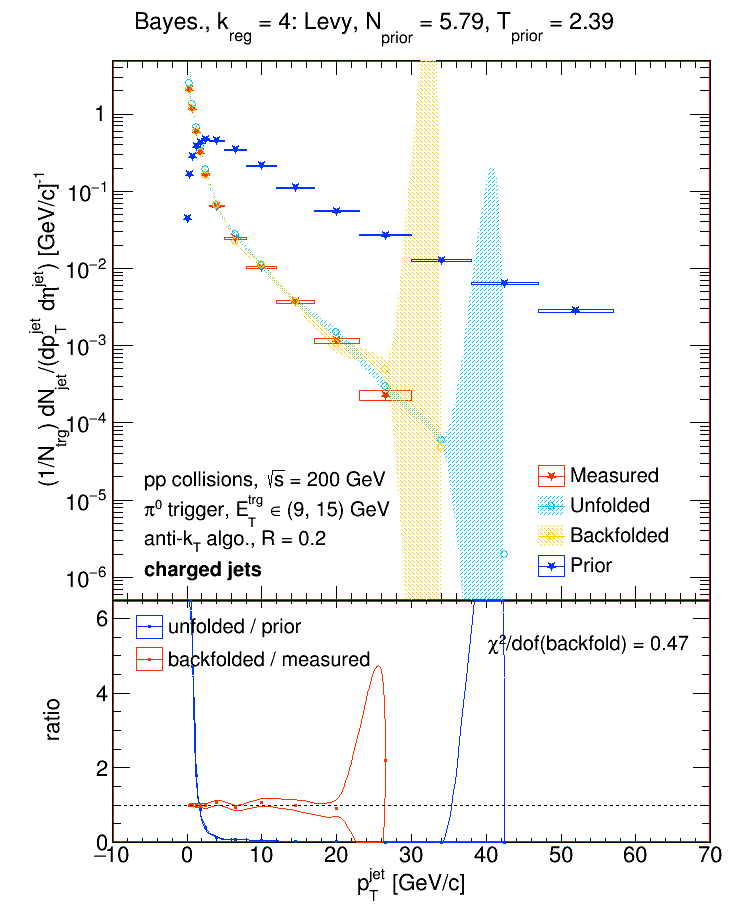
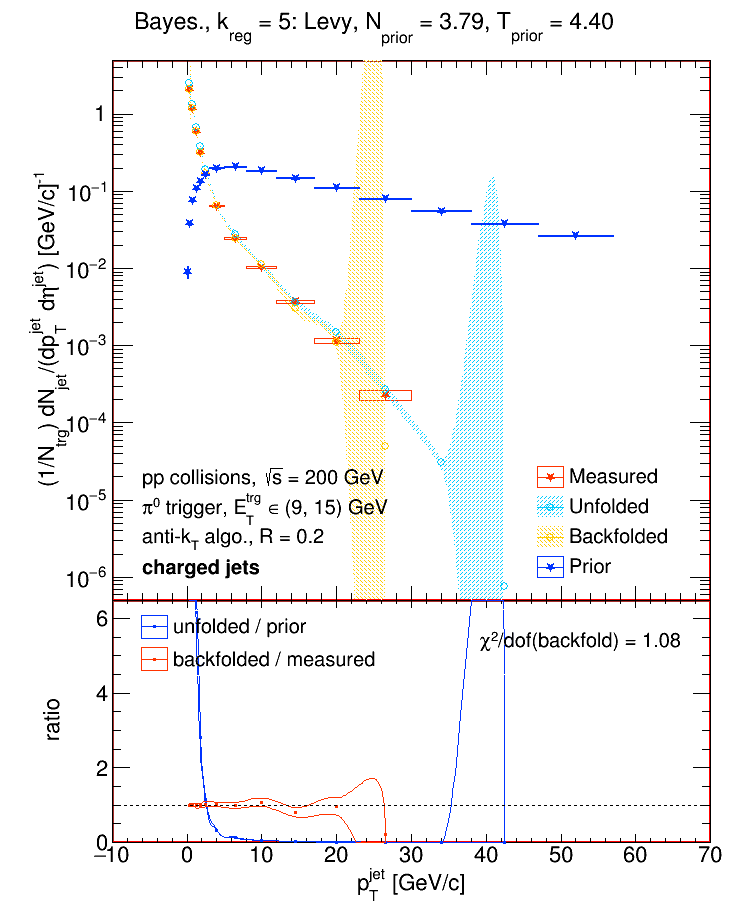
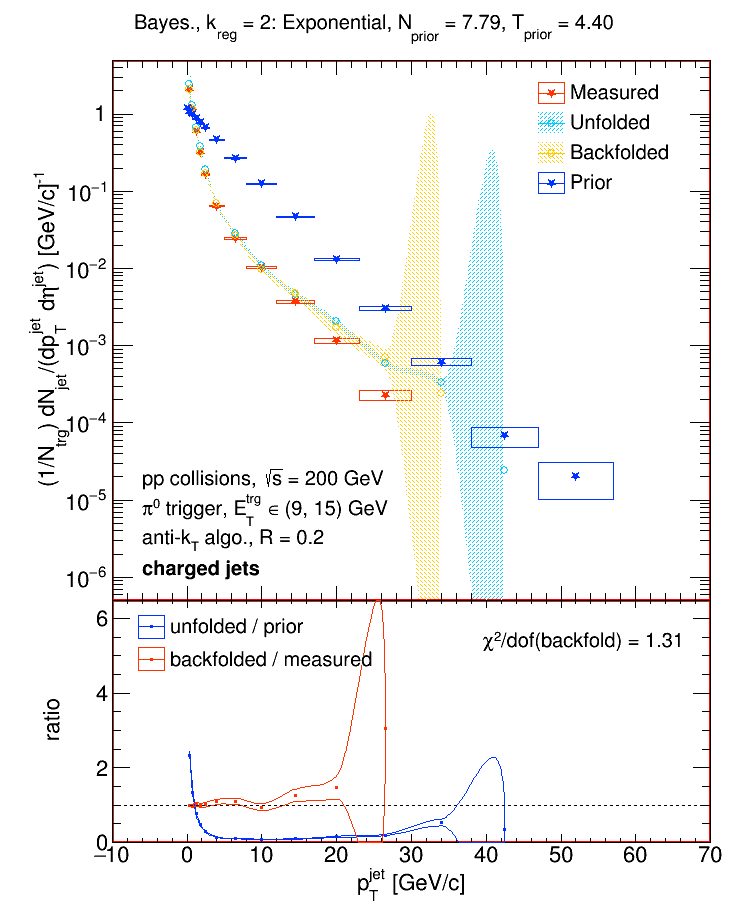
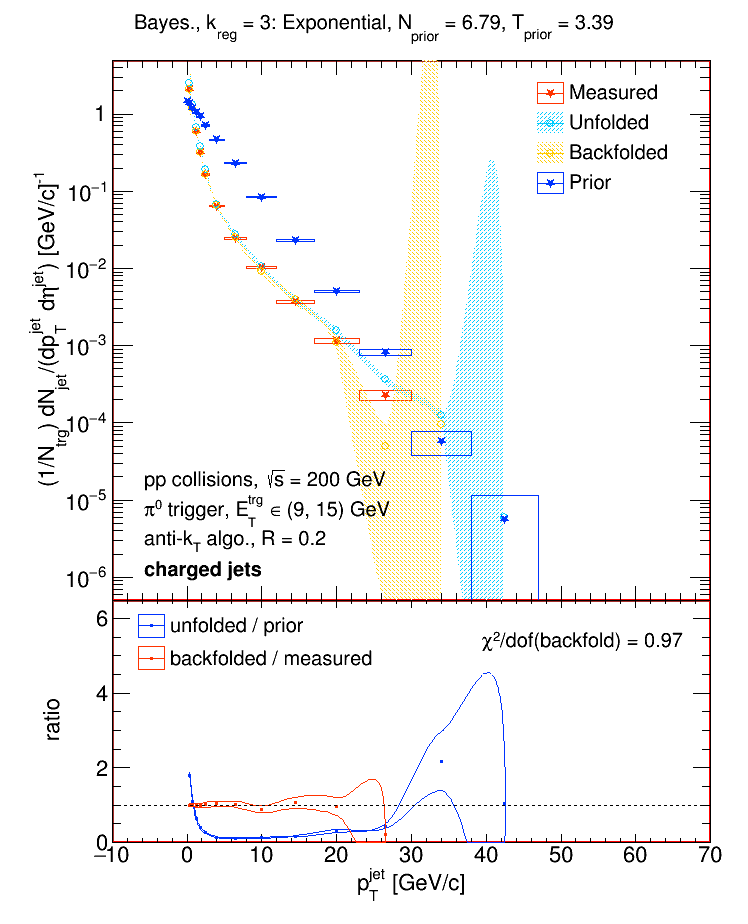
Note: the 'n' and 't' values in the plots above are slightly off.  Add 0.01 to get the actual values!