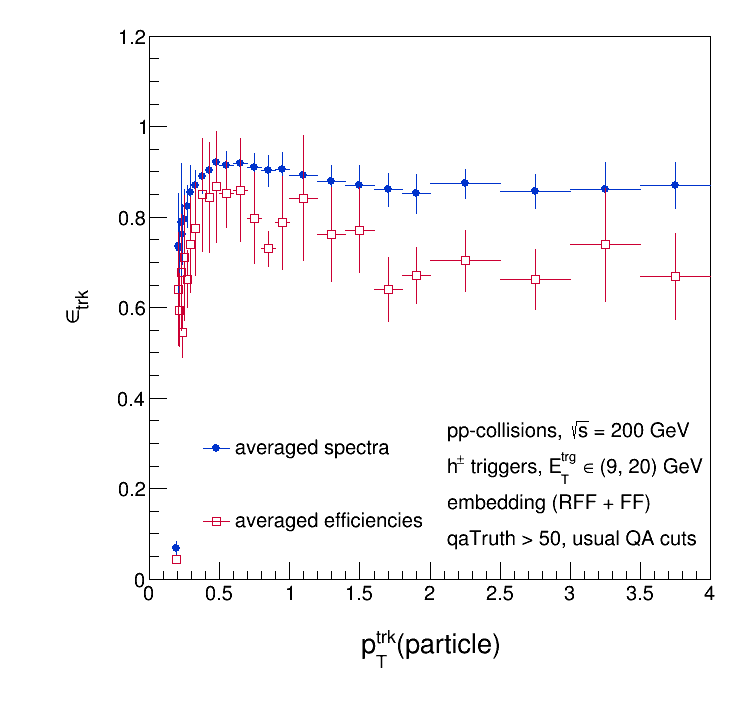
This is a brief interlude in my journey to figure out what's different between our Pythia8 simulation and embedding.  I wanted to see if it mattered one way or the other with how I calculated the average tracking efficiency over all pTparton bins.  The plots below compare two different methods: (1) averaging the particle and detector spectra and then taking the ratio, and (2) calculating the ratio for each pTparton bin and then averaging the ratios.

So to spell things out, here's the algorithm for method (1):

1. Match particle-level tracks to detector-level tracks and fill relevant histograms as a function of particle pTtrk.
2. Sum particle- and detector-level pTtrk distributions, weighted according to relevant pTparton bin.
3. Normalize the summed distributions by the (scaled) number of triggers.
4. Take the ratio of the averaged detector-level pTtrk distribution to the averaged particle-level pTtrk distribution.

The normalization in step 3 is arbitrary, and will cancel out when taking the ratio in step 4 since the number of triggers is the same between the particle- and detector-levels.  This algorithm produces an efficiency that looks like so:

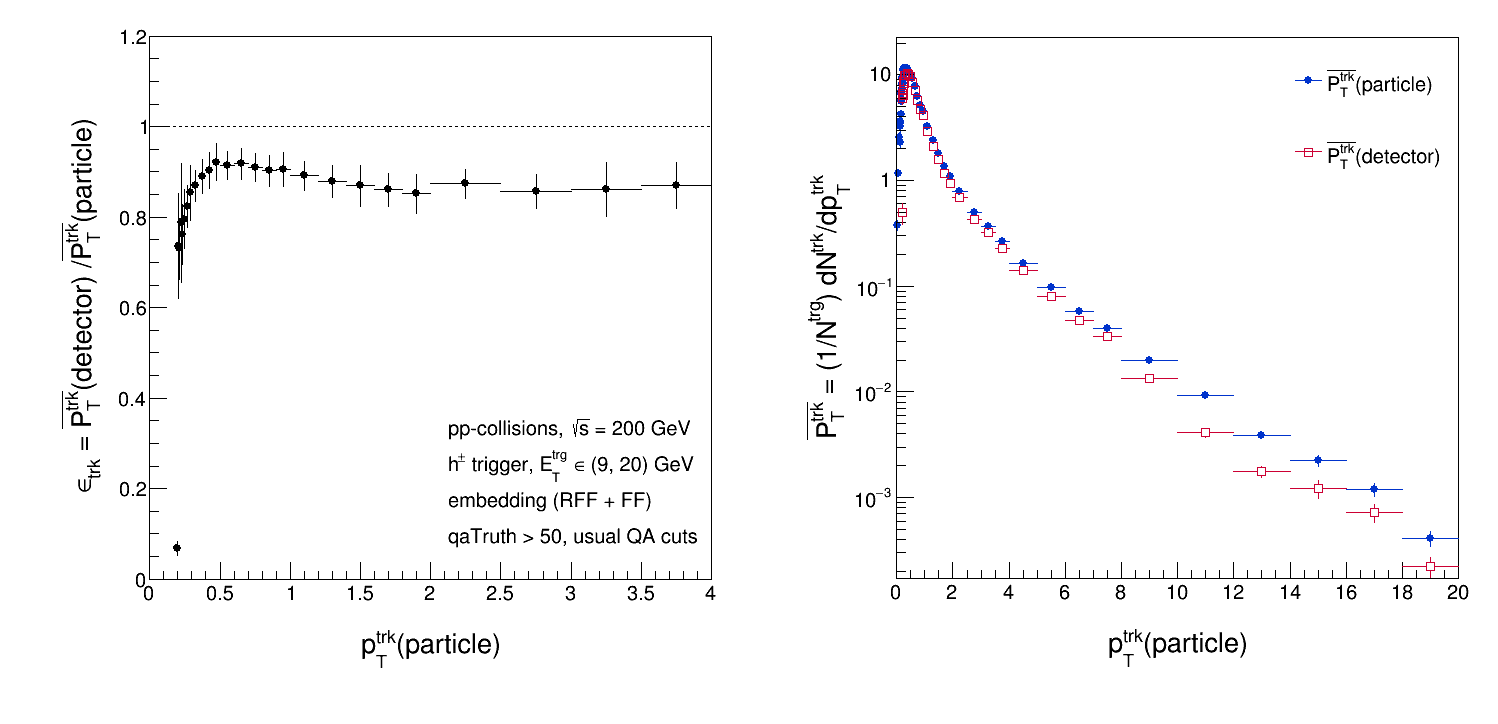
The slight depression in the track spectrum from 9 - 20 GeV/c is due to the trigger selection.  The other algorithm proceeds as such:

1. Match particle-level tracks to detector-level tracks and fill relevant histograms as a function of particle pTtrk.
2. For each pTparton bin, take the ratio of the detector-level pTtrk distribution to the particle-level pTtrk distribution.
3. Take the geometric mean of ratios over all pTparton bins.

In hindsight, I probably should've weighted each ratio by the relevant factor for each pTparton bin.  Either way, this procedure produces an efficiency like below.

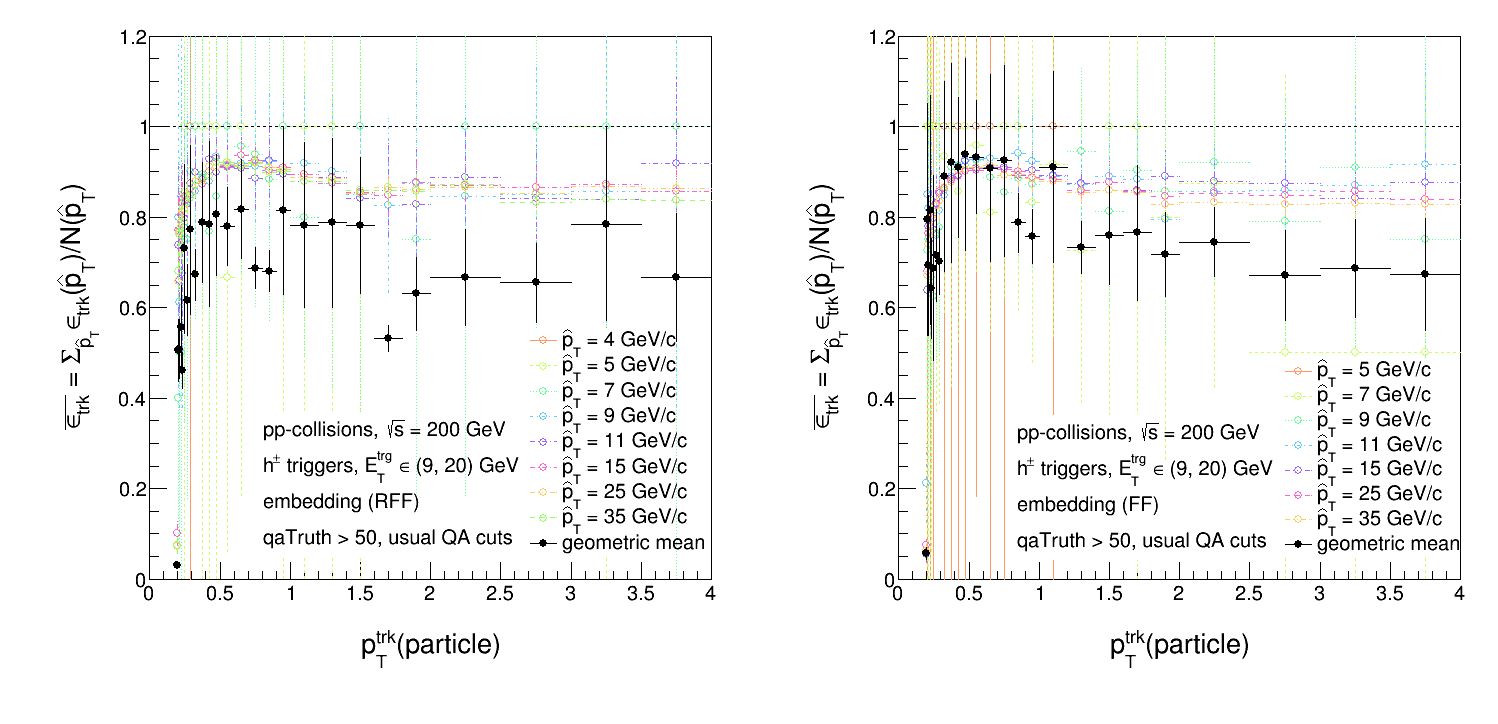
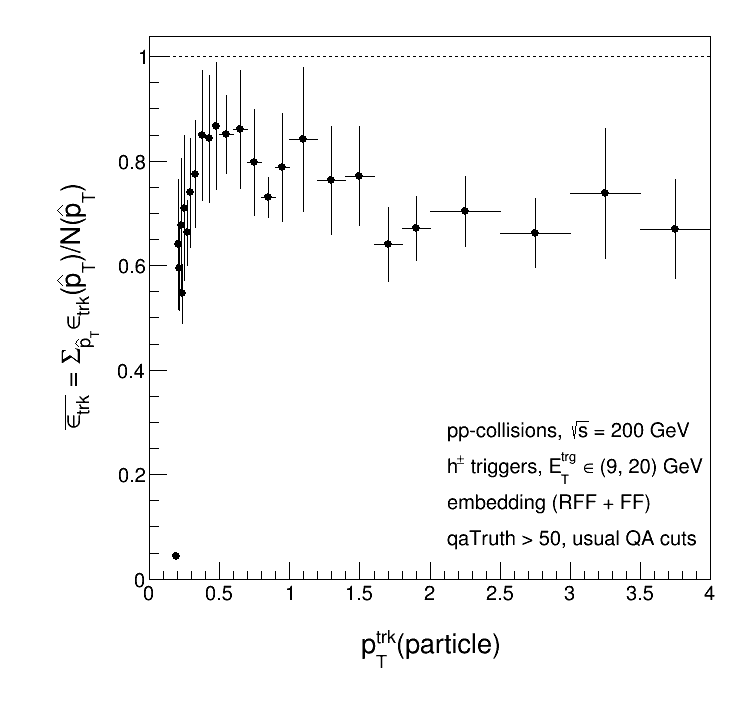
The 1st method looks quite a bit more reasonable, which is good.  Method (1) is what I've been doing up until now.  The two efficiencies on top of each other are shown below.